이 문제를 풀기 위해서 꽤 많은 시간이 들었다.
일단 수학적으로 접근을 해야하기 때문에 패턴을 파악하고 패턴을 수식화하는 능력이 필요하다.
그럼 일단 패턴을 분석해서 식을 도출해 보자.
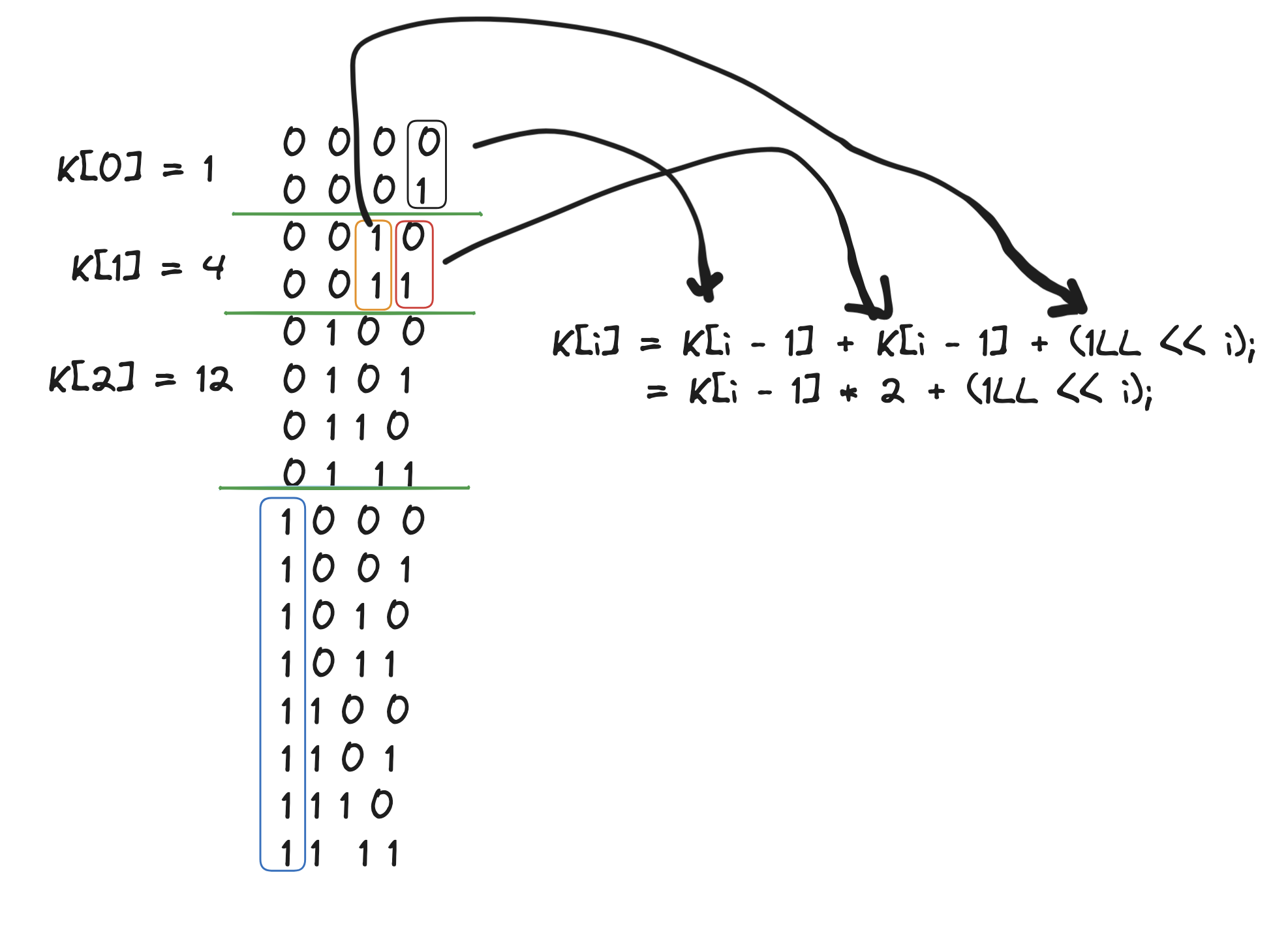
0010이 되기 위해서는 0000, 0001을 지나쳐야하고 1의 개수는 총 1개이다.
0100이 되기 위해서는 0000, 0001, 0010, 0011을 지나쳐야하고 총 4개이다.
위 사진을 보면 0100, 0010같이 2의 배수인 자리에서 그 위에 1이 몇개인지 알 수 있는 수학 패턴 식을 구할 수 있다.
K[i] = K[i - 1] * 2 + (1LL << i);
위 같은 식이 나온다. 여기서 1LL은 long long 타입의 1을 나타낸다.
그렇다면 2의 배수로 딱 떨어지는 수가 아닌 경우에는 어떻게 나머지 1의 개수를 구할 수 있을까?
그 방법은 이렇다.
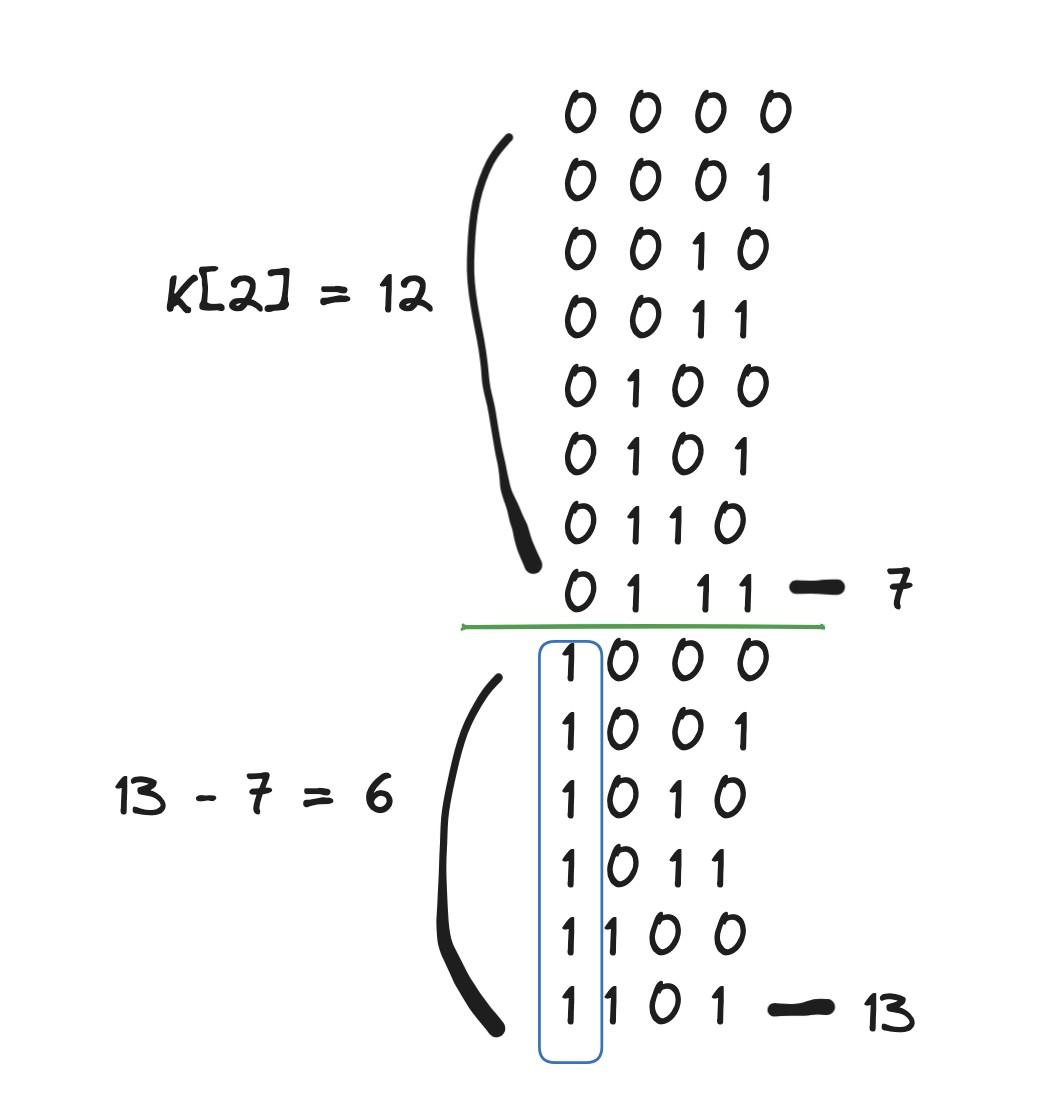
만약에 0~13까지의 1의 총 개수를 구하고 싶은데 1000 이전까지는 패턴으로 1의 개수를 K[2] 로 알 수 있지만 나머지를 계산하려면
13 - 7를 뺀 개수로 알 수 있고 이를 공식으로 나타내면 X - (1LL << i) + 1 이다.
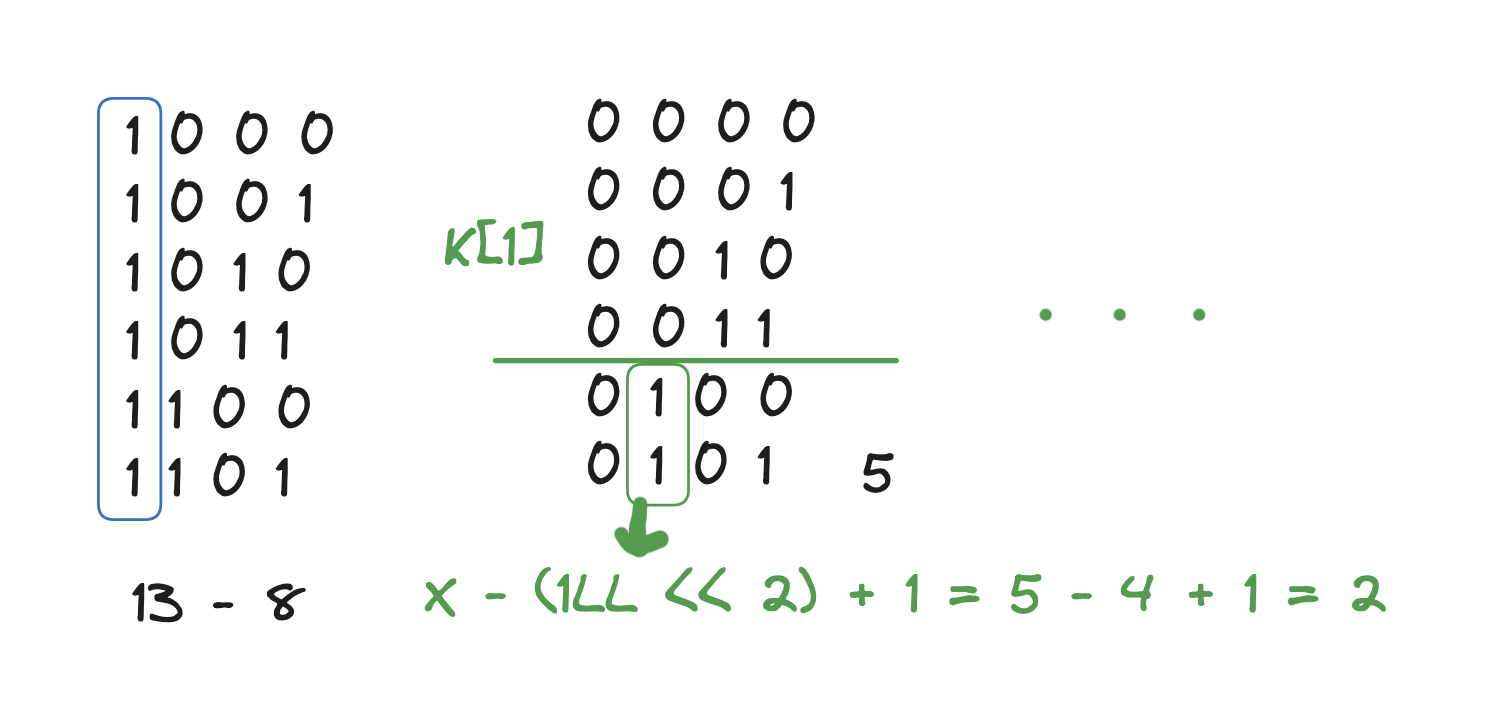
이미 구한 부분은 지우도 같은 패턴으로 계속 값을 구하다보면 0~13까지의 1의 개수를 구할 수 있다.
(설명하기가 꽤 힘드네요... 이해가 안되신다면 죄송합니다.. ㅎㅎ)
그래서 코드는 이렇게 나온다.
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
long long K[55];
void setK(){
K[0] = 1;
long long mul = 1;
for (long long i = 1; i < 55; i++){
mul *= 2;
K[i] = mul + K[i - 1] * 2;
}
}
long long countAllOne(long long x){
long long result = x & 1;
for (int i = 54; i > 0; i--){
if (x & (1LL << i)) {
result += K[i - 1] + (x - (1LL << i) + 1);
x -= 1LL << i;
}
}
return result;
}
int main(){
long long A, B;
cin >> A >> B;
setK();
cout << countAllOne(B) - countAllOne(A - 1) << endl;
return 0;
}'코딩테스트' 카테고리의 다른 글
| [백준 2212] 센서, C++ (0) | 2024.03.04 |
|---|---|
| [백준 골드5 2240] 자두 나무, C++, DP (1) | 2024.02.28 |
| [SQL] 프로그래머스 : 재구매가 일어난 상품과 회원 리스트 구하기 (0) | 2024.02.20 |
| [C++, 코딩테스트] 프로그래머스 : 의상 with 해시 (0) | 2024.02.16 |
| [C++, 코딩테스트] 프로그래머스 : 큰 수 만들기 with 그리디 (0) | 2024.02.16 |
